Note
Go to the end to download the full example code
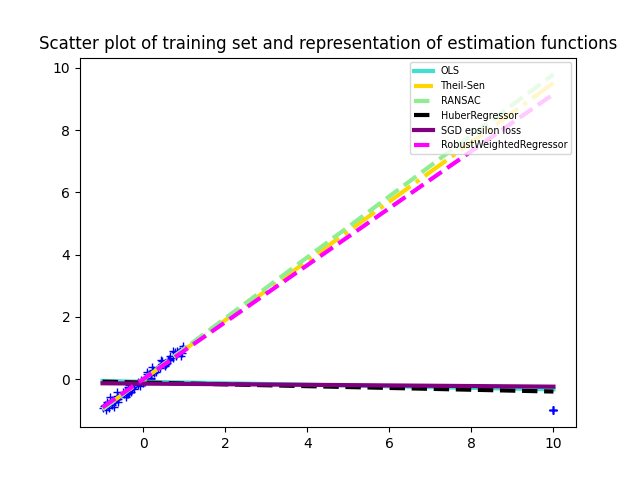
Robust regression on simulated corrupted dataset¶
In this example we compare the RobustWeightedRegressor with various robust regression algorithms from scikit-learn.
import matplotlib.pyplot as plt
import numpy as np
from sklearn_extra.robust import RobustWeightedRegressor
from sklearn.utils import shuffle
from sklearn.linear_model import (
SGDRegressor,
LinearRegression,
TheilSenRegressor,
RANSACRegressor,
HuberRegressor,
)
# Sample along a line with a Gaussian noise.
rng = np.random.RandomState(42)
X = rng.uniform(-1, 1, size=[100])
y = X + 0.1 * rng.normal(size=100)
# Change the 5 last entries to an outlier.
X[-5:] = 10
X = X.reshape(-1, 1)
y[-5:] = -1
# Shuffle the data so that we don't know where the outlier is.
X, y = shuffle(X, y, random_state=rng)
estimators = [
("OLS", LinearRegression()),
("Theil-Sen", TheilSenRegressor(random_state=rng)),
("RANSAC", RANSACRegressor(random_state=rng)),
("HuberRegressor", HuberRegressor()),
(
"SGD epsilon loss",
SGDRegressor(loss="epsilon_insensitive", random_state=rng),
),
(
"RobustWeightedRegressor",
RobustWeightedRegressor(weighting="mom", k=7, random_state=rng),
# The parameter k is set larger to the number of outliers
# because here we know it.
),
]
colors = {
"OLS": "turquoise",
"Theil-Sen": "gold",
"RANSAC": "lightgreen",
"HuberRegressor": "black",
"RobustWeightedRegressor": "magenta",
"SGD epsilon loss": "purple",
}
linestyle = {
"OLS": "-",
"SGD epsilon loss": "-",
"Theil-Sen": "-.",
"RANSAC": "--",
"HuberRegressor": "--",
"RobustWeightedRegressor": "--",
}
lw = 3
x_plot = np.linspace(X.min(), X.max())
plt.plot(X, y, "b+")
for name, estimator in estimators:
estimator.fit(X, y)
y_plot = estimator.predict(x_plot[:, np.newaxis])
plt.plot(
x_plot,
y_plot,
color=colors[name],
linestyle=linestyle[name],
linewidth=lw,
label="%s" % (name),
)
legend = plt.legend(loc="upper right", prop=dict(size="x-small"))
plt.title(
"Scatter plot of training set and representation of"
" estimation functions"
)
plt.show()
Total running time of the script: ( 0 minutes 0.232 seconds)